CHALLENGE ESCRITURA NOVIEMBRE

 ❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤

REPASO DE POTENCIAS (en clase)

 

Repaso multiplicaciones por 3 cifras.

 

FICHA DE REPASO DE MATES

 

FICHA DE REPASO DE LENGUA

 

REPASO MULTIPLICACIONES POR DOS O TRES CIFRAS

¡HOLA CHICOS! Vamos a repasar un poco... Los que tengáis dudas tenéis que leer atentamente estas instrucciones. Los que ya tenéis claro cómo multiplicar por dos o tres cifras podéis pasar directamente a los ejercicios de snappet. No obstante, no estaría mal que también le echéis un ojo 👀

En este post vamos a aprender a multiplicar por dos y tres cifras.

Antes de comenzar vamos a repasar cuales son los términos de la multiplicación.

Términos de la multiplicación

• Factores: Los factores son los números que se multiplican.
• Producto: El producto es el resultado de la multiplicación.
• Multiplicando: El multiplicando es el factor que se encuentra arriba en la multiplicación.
• Multiplicador: El multiplicador es el factor que se encuentra debajo del multiplicando.

Normalmente el multiplicando es mayor que el multiplicador.

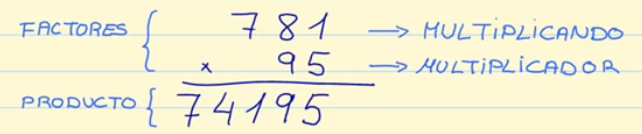
Ahora vamos a ver cuales son los pasos para hacer una multiplicación de 2 y 3 cifras.

Pasos para hacer una multiplicación de 2 y de 3 cifras

1. Multiplicar las unidades del multiplicador por el multiplicando y el resultado escribirlo en la fila de abajo.

Vamos a ver un ejemplo. Si multiplicamos 781 x 95, lo primero que hay que hacer es multiplicar por 5, que son las unidades de 95, por cada una de las cifras del multiplicando de derecha a izquierda y poner el resultado, 3905, en la fila de abajo, como muestra la imagen.

2. Multiplicar las decenas del multiplicador por el multiplicando y el resultado escribirlo en la fila de abajo pero desplazado una posición a la izquierda.

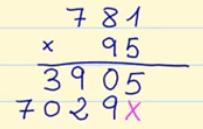
Seguimos con el ejemplo. Ahora multiplicamos el 9, ya que son las decenas del multiplicador 95, por el multiplicando 781. El resultado 7029 habrá que escribirlo debajo de 3905 pero desplazándolo una posición hacia la izquierda.

3. Sumar los productos.

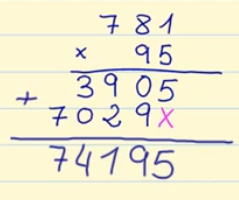
Como vemos en la imagen sumamos los productos y el resultado de la multiplicación es 74.195

Si el multiplicador es de tres cifras, el resultado de la multiplicación de las centenas se escribirá desplazado dos posiciones hacia la izquierda. Vamos a ver otro ejemplo. 

Si multiplicamos 367 x 251, lo primero que hay que hacer es multiplicar las unidades de 251, es decir, 1, por 367. El resultado sería 367 y lo ponemos en la fila de abajo.

Después multiplicamos las decenas de 251, es decir, 5, por 367. El resultado sería 1835 y lo ponemos en la fila de debajo pero una posición desplazado hacia la izquierda.

A continuación multiplicamos las centenas de 251, es decir, 2, por 367. El resultado sería 734 y lo ponemos en la fila de debajo pero dos posiciones desplazado hacia la izquierda.

Finalmente, hacemos la suma y el producto es 92.117

TENEMOS UNA LECCIÓN NUEVA EN SNAPPET: MULTIPLICACIÓN POR NÚMEROS DE VARIAS CIFRAS.

 ES CONVENIENTE QUE LA HAGÁIS UTILIZANDO EL CUADERNO AL LADO para ayudaros hacer las operaciones con lápiz y goma. Si lo hacéis solo con la tablet va a ser muy complicado y os podéis liar. ¡Utilizad el cuaderno!

22 de octubre- LITERATURA

 

¿QUÉ ES LA LITERATURA?

ESQUEMA EN EL CUADERNO DE ESQUEMAS (APARTADO DE LITERATURA)

DICTADO:

EJERCICIO EN EL CUADERNO:

Coloca la tilde en las palabras que lo requieran e indica si es aguda, llana o esdrújula.

22 de oct- repaso- APROXIMACIÓN DE NÚMEROS (a la decena, centena, ud. millar...)

 

Aproximación a la Decena / a la Centena / a la Unidad de Millar

1.- Aproximación a la decena

Aproximar un número a la decena es buscar un número múltiplo de 10 (su última cifra es un cero) que más se le aproxime:

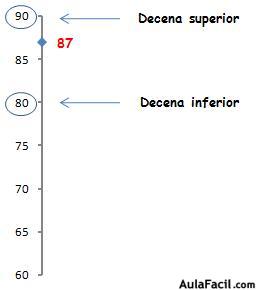
Por ejemplo, el número 87:

 

 

Su decena inferior es 80 y su decena superior es 90. Ahora se trata de ver a cual de ellas se aproxima más, a la inferior o a la superior:

Si el número termina en una cifra inferior a 5 se aproxima a la decena inferior.

En cambio si termina en 5 o en una cifra superior se aproxima a la decena superior.

Nuestro número, 87, termina en 7. Esta cifra es mayor que 5 por lo que lo aproximaremos a la decena superior.

De hecho se puede ver en el gráfico que 87 está más cerca de 90 que de 80.

Veamos otro ejemplo:

42:

 

 

El múltiplo de 10 más cercano por debajo es 40 y el más cercano por arriba es 50.

Vemos que el número termina en 2; al ser una cifra inferior a 5 hay que aproximarlo a la decena inferior, es decir a 40.

Se puede ver en el gráfico que 42 está más cerca de 40 que de 50.

2.- Aproximación a la centena

Aproximar un número a la centena es buscar un número múltiplo de 100 (sus dos últimas cifras son cero) que más se aproxime al número en cuestión.

Si el número termina en una cifra inferior a 50 se aproxima a la centena inferior. En cambio, si termina en 50 o en una cifra superior se aproxima a la centena superior.

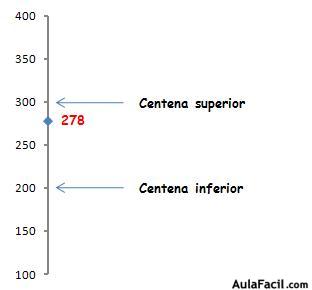
Veamos un ejemplo: el número 278.

 

 

Vemos que 278 se encuentra entre las centenas 200 y 300, pero que está más cerca de esta última. Por lo tanto lo aproximaremos a 300.

De hecho, 278 termina en 78 que es superior a 50, por lo que lo aproximamos a la centena superior.

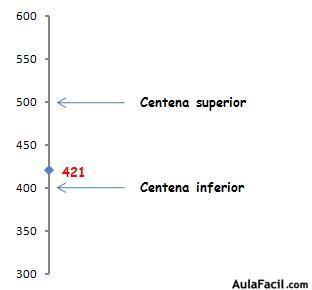
Vamos a ver otro ejemplo: 421.

 

 

421 se encuentra entre las centenas 400 y 500, pero está más cerca de la primera. Por lo tanto lo aproximaremos a 400.

De hecho, 421 termina en 21 que es inferior a 50, por lo que lo aproximamos a la centena inferior.

3.- Aproximación a la unidad de millar

Aproximar un número a la unidad de millar es buscar un número múltiplo de 1.000 (sus tres últimas cifras son cero) que más se aproxime al número en cuestión.

Si el número termina en una cifra inferior a 500 se aproxima a la unidad de millar inferior. En cambio, si termina en 500 o en una cifra superior se aproxima a la unidad de millar superior.

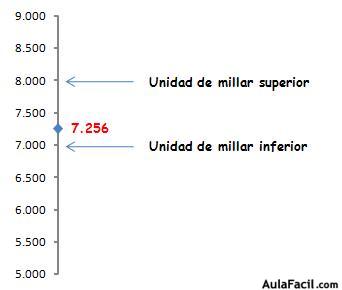
Veamos un ejemplo: el número 7.256.

 

 

Vemos que 7.256 se encuentra entre las unidades de millar 7.000 y 8.000, pero que está más cerca de la primera. Por lo tanto lo aproximaremos a 7.000.

De hecho, 7.256 termina en 256 que es inferior a 500, por lo que lo aproximamos a la unidad de millar inferior.

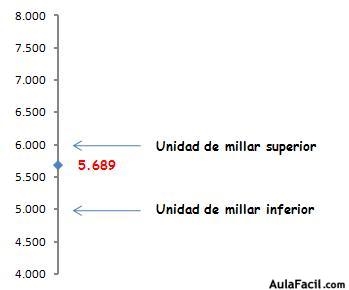
Vamos a poner otro ejemplo: 5.689.

 

 

5.689 se encuentra entre las unidades de millar 5.000 y 6.000, pero está más cerca de la segunda. Por lo tanto lo aproximaremos a 6.000.

De hecho, 5.689 termina en 689 que es superior a 500, por lo que lo aproximamos a la unidad de millar superior.

 

EJERCICIOS:

--------------------> ¡¡¡SEGUIMOS CON SNAPPET!!!!

21 de oct- repaso. MULTIPLICAR POR 10, 100, 1000

 ¡HOLA!

Vamos a repasar un poco esto que hicimos en clase, y aumentando un pelín la dificultad.

Multiplicar un Número natural o Decimal por 10; 100; 1000...
*Para multiplicar un número natural solamente se agrega uno, dos o tres ceros al número dado.
*Para multiplicar un número decimal por la unidad seguida de ceros (10; 100; 1000...) se desplaza la coma hacia la DERECHA tantos lugares como ceros acompañen a la unidad.

Ejemplos:
Efectuar las siguientes multiplicaciones:

a) 17 X 100   =  1700
b) 2648 X 10  = 26480
c) 4 X1000  = 4000
d) 8453 X 100 = 845300
e) 6398 X10000 = 63980000
En los cinco ejercicios anteriores sólo agregué ceros:
Se multiplicó por 10 agregué un 0
Se multiplicó por 100 agregué  00
Se multiplicó por 1000 agregué 000
Se multiplicó por 10000 agregué 0000

¡FACILÍSIMO!

Ahora multipliquemos un decimal:
En el resultado se escribe el mismo número pero...cuidado con la coma.

Ejemplos:
LA COMA SE MUEVE HACIA LA DERECHA.

a) 83,549 X 10 = 835,49
La coma la trasladé un lugar porque hay un 0
b) 7,8542 X 1000 = 7854,2
La coma la trasladé tres lugares porque hay tres 000
c) 5,4876 X 100 = 548,76
La coma la trasladé dos lugares porque hay dos 00
d) 365,15628 X 10000= 3651562,8
La coma la trasladé cuatro lugares porque hay cuatro 0000.

Para multiplicar un número decimal por 10, 100, 1000… lo único que tendremos que hacer es mover la coma del decimal a la derecha tantas posiciones como ceros tenga el número.

Por ejemplo:

Como el 100 tiene dos ceros moveremos la coma dos posiciones a la derecha. Por lo tanto, el resultado es 315,4

 ¿Y DIVIDIR? ¿CÓMO LO HAGO? ATENTOS...

Dividir números decimales por 10, 100, 1000…

Para dividir un número decimal por 10, 100, 1000… lo único que tendremos que hacer es mover la coma del decimal a la IZQUIERDA tantas posiciones como ceros tenga el número.

Por ejemplo:

Como el 10 tiene un cero moveremos la coma una posición a la izquierda. Por lo tanto, el resultado queda 8,42

Ejemplos:
Efectuar las siguientes divisiones:
LA COMA SE MUEVE HACIA LA IZQUIERDA.
a) 1235,97 : 100 = 12,3597
La coma la trasladé dos lugares porque hay dos 00
b) 625 : 10 = 62,5
625 es un número entero, la coma no se ve pero  está a la derecha del 5. La coma la trasladé un lugar porque hay un 0
c) 21,3 : 1000 = 0,0213
La coma la trasladé tres lugares porque hay tres 000
d) 71,4 : 100 = 0,714
La coma la trasladé dos lugares porque hay dos 00
e) 2981,2: 1000 = 2,9812
La coma la trasladé tres lugares porque hay tres 000
f) 4 : 100 = 0,04

¡¡¡ VAMOS HACER EJERCICIOS!!! ¡¡ A POR TODAS!!

Si aún tenéis un poco de dudas con las divisiones os propongo ver el siguiente video (ES MUY BUENO)

PRIMERO multiplicaciones x 10, 100, 1000

AHORA dividir entre 10, 100, 1000

¡¡¡¡¡¡¡¡¡SOIS GENIALES!!!!!!!!!!!! ¡¡¡ÁNIMO!!!!